k-近邻算法
原理
(k-nearest neighbor),是一个基本分类与回归方法。存在一个样本数据集合,也称作为训练样本集,并且样本集中每个数据都存在标签,即我们知输道样本集中每一个数据与所属分类的对应关系。入没有标签的新数据后,将新的数据的每个特征与样本集中数据对应的特征进行比较,然后算法提取样本最相似数据(最近邻)的分类标签。
特征以距离度量(欧式距离):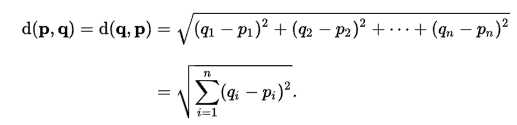
k-近邻算法步骤如下:
1.计算已知类别数据集中的点与当前点之间的距离;
2.按照距离递增次序排序;
3.选取与当前点距离最小的k个点;
4.确定前k个点所在类别的出现频率;
5.返回前k个点所出现频率最高的类别作为当前点的预测分类。
流程:
- 数据解析:将待处理数据的格式改变为分类器可以接收的格式(特征矩阵和对应的分类标签向量)
- 数据可视化
- 数据归一化:特征值属性对计算结果的影响不同,可进行权重分配。
- 数值归一化:newValue = (oldValue - min) / (max - min),其中min和max分别是数据集中的最小特征值和最大特征值。
- 测试算法(验证分类器)
优点
- 简单好用,容易理解,精度高,理论成熟,既可以用来做分类也可以用来做回归;无需参数估计,无须训练;
- 可用于数值型数据和离散型数据;
- 训练时间复杂度为O(n);无数据输入假定;
- 对异常值不敏感,对噪声不敏感
缺点
- 计算复杂性高;空间复杂性高;
- 样本不平衡问题(即有些类别的样本数量很多,而其它样本的数量很少);
- 一般数值很大的时候不用这个,计算量太大。但是单个样本又不能太少,否则容易发生误分。计算每一个待分类样本要与全体已知样本计算距离,才能得到k个最近邻点;
- 最大的缺点是无法给出数据的内在含义。(可解释性差)
算法改进
- 消除维数灾难(出现不相关或相关性低的的属性,欧式距离会不准确,消耗大量计算资源:消除不相关属性即特征选择;属性加权。
- 快速KNN算法:将样本进行排序,在所有有序的样本队列中搜索k个最邻近样本,从而减少搜索时间/